人工智能路径规划算法？

发布时间：2024-08-12 03:17:13 人气：

本人人工智能零基础，刚被研究生院校录取，老师布置任务是学习人工智能原理及应用的路径规划算法，求问各路大神该如何下手？

摘要：运动规划是移动机器人自主导航系统中的重要模块之一，相关算法研究成果层出不穷，本文将智能仿生规划算法拆解为三个子类算法：神经网络规划算法、模糊逻辑规划算法及基于仿生的规划算法，并沿时间顺序概述相关算法的发展历程，最后从实时性、环境适应能力及学习能力等方面分析了上述三类算法的优缺点。

01引言

在前文《机器人图规划算法研究现状简述》中，结合图 1.1对“运动规划是什么？要解决什么问题？”这两个问题有详细阐述，并概述了运动规划与运动控制模型、环境感知这两个部分之间的关系。

图 1.1 运动规划示意图（图片来源：http://wiki.ros.org/navigation）

从上述可知，要进行运动规划，需要有两个前提条件：地图和定位。机器人需要先利用传感器获取环境信息，构建环境地图并计算自身在环境地图中的位姿（见《机器人环境感知研究现状简述》），接着根据自身在地图中的位置，明确起始点和终点后，才可以进入到运动规划阶段，最后将生成的轨迹转化为运动控制命令发送给运动控制模型（见《常见移动机器人运动学模型总结》），驱动机器人运动。

如图 1.2所示，运动规划的研究主要是对多目标多变量多约束耦合的规划模型优化求解。对于具有非完整约束的移动机器人而言（见《两轮差速驱动机器人运动模型及应用分析》），在分布有障碍物的环境中求解最优路径是NP-hard问题，即对于任意场景无法保证在多项式时间内求得最优解，因此大部分规划算法追求次优解或局部最优[1]。

诸多学者针对不同应用场景和需求，设计、改进了非常多的运动规划算法，其中常见的运动规划算法主要包括四类：图规划算法、空间采样算法、曲线插值拟合算法和仿生智能算法，通过规划模型求解得到最佳轨迹曲线，包含无碰撞顺滑的路径曲线和平滑的速度曲线，并输入到控制器驱动机器人运动。

本文将对智能仿生算法领域的研究进展及成果进行分类阐述，主要概述同族算法的发展过程，不对具体算法展开分析，在后续系列文章会挑选部分经典常用算法深入剖析。

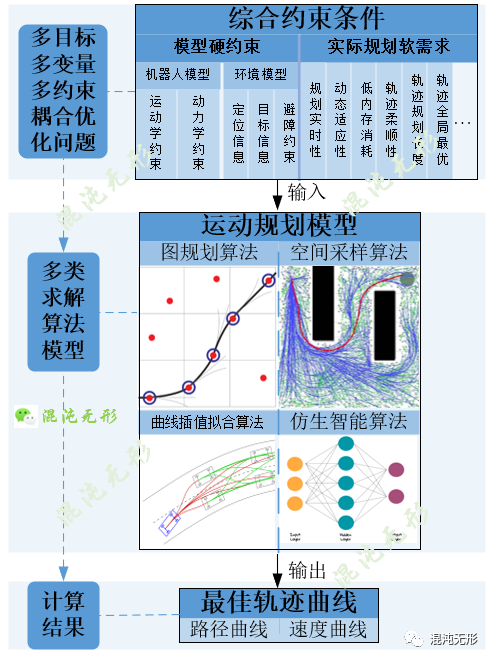
图 1.2 运动规划通用模型

02智能仿生规划算法研究分析

针对机器人运动规划问题，除上述基于经典模型的规划算法外（《图规划算法》、《空间采样算法》和《曲线插值拟合算法》），还有神经网络、模糊逻辑及基于自然灵感的算法（遗传算法、粒子群算法、蚁群算法等），并逐渐成为研究热点。

与经典算法相比，智能算法能够较好适应复杂动态环境中的不确定、不完整的信息，但需要前期学习阶段和较高计算成本，适用于大型机器人，如无人车等。

2.1神经网络规划算法

利用神经网络对机器人导航任务的输入、输出之间的复杂关系进行建模。如文献[2]提出了一种通过模仿学习过程构建机器人目标导向导航环境内部模型的分层结构。该方法以训练递归神经网络RNN的回声状态网络（Reservoir Computing）为基础。它由两个随机生成的RNN组成，一个用于建模定位，另一个用于学习导航。训练后的系统能够在较大的未知环境中定位，并成功导航至目标点。

另一方面，D. Janglova[3]使用主分分析(PCA)和多层感知器(MLP)两个神经网络构建了无碰撞路径。PCA是无监督线性过程，可将大量数据过滤转化为少数几个主要的无碰撞区域成分，并通过MLP输出转向角控制指令。

图 2.1 PCA和MLP网络拓扑结构

M.A. Sagban等人提出了一种在非结构化室内[4]环境下基于反应性导航算法的神经网络方法。该方法将离线学习和在线学习相结合，达到最佳的学习效果。

在文献[5]中，采用神经网络反向传播算法对机器人进行在线训练，使机器人能够避开移动的障碍物。但神经网络在运动规划中的应用仍然存在一些问题：神经网络计算通常很耗时，且不能保证收敛到最优解。

2.2模糊逻辑规划算法

除神经网络外，模糊逻辑可模仿人感知能力以适应环境中的不确定性。

Chang和T. Jin提出了一种模糊推理模型来解决移动机器人路径规划问题[6]。通过传感器感知机器人在未知动态环境下的目标/障碍物位置和当前速度。在模型中,三个主要的导航目标:目标取向(寻求目标),避障(避免障碍)和旋转运动(保持航向)都包含在一个成本函数找到最优的转向角θ。移动机器人通过根据环境改变成本函数的权重来实现智能导航(图 2.2)。

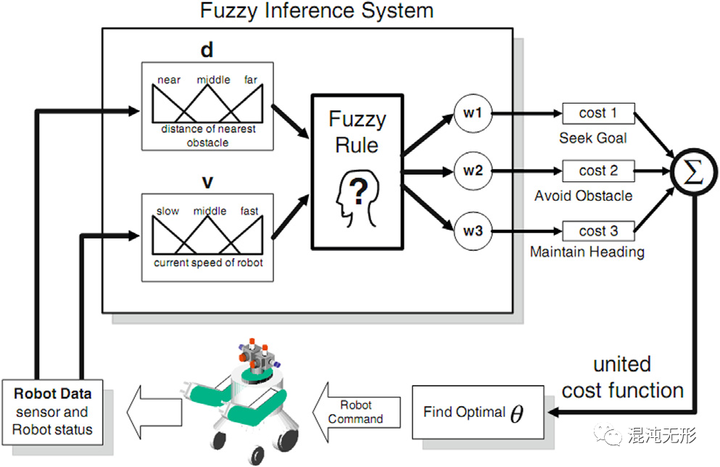
图 2.2 路径规划模糊系统架构[6]

在文献[7]中设计了一个包含48条模糊规则的模糊逻辑系统，包括目标寻找、避障和障碍物跟随三种行为。多个传感器的组合用于感知机器人附近的障碍物、目标位置和当前机器人的速度。因此，该移动机器人能够较好地看清所处的环境，自主避开静态和动态障碍物。它可以在各种情况下生成合理的目标路径，而不存在对称的不确定性和死循环问题。如前所述，模糊逻辑具有模拟语言变量所代表的人类思维和规则所代表的知识库的能力。然而，它在选择最合适的规则和成员函数方面存在困难。

2.3基于仿生的规划算法

受生物行为启发，将仿生算法应用于求解复杂运动规划问题能够得到良好的效果。

遗传算法

遗传算法是一种基于自然遗传学的优化工具，它利用了自然选择、交叉和突变等过程的优点。遗传算法在解决组合优化问题方面具有很大的潜力，如复杂环境下路径规划问题。

文献[8]遗传算法用于路径规划领域，并结合了小规模局部搜索，以适用于动静态环境。

文献[9]提出了一种基于遗传算法的动态路径规划算法(dynamic path planning algorithm, DPPA)，可在U形、V形等套状障碍物中，或遇到动态障碍物的情况，生成可行的路径。

如图 2.3所示，文献[10]提出改进的GA-Fuzzy-A*混合算法，使用改进的遗传算法和改进的A*算法得到最优路径，接着输入模糊控制器生成基于时间的轨迹，在动态避障方面有良好表现。

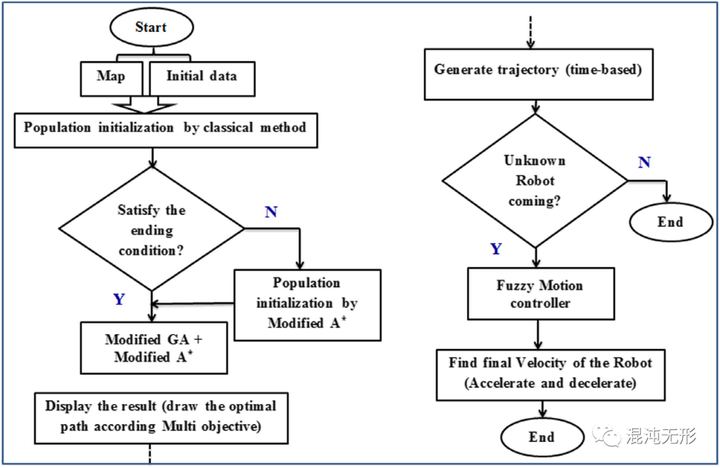
图 2.3 GA-Fuzzy-A*混合算法[10]

粒子群算法

与GA相似，PSO模仿鸟群觅食，通过粒子自我体验与社会经验迭代更新。

文献[11]中，Y. Zhang等人提出了一种不确定环境下基于PSO的多目标机器人路径规划算法，目标函数由风险度和路径距离组成，因此，路径规划问题被认为是一个具有不确定系数的约束双目标优化问题。

极坐标PSO (polar coordination PSO, PPSO)用于动态环境下的机器人路径规划[12]，该算法将任务分解为全局规划阶段和局部规划阶段。它可以根据静态障碍物信息寻找全局最优路径。然后，采用在线实时路径规划策略，通过预测障碍物的未来位置来避开移动障碍物。

蚁群算法

蚁群算法与PSO算法均属于通过群体行为实现数据聚类的算法。在[13]中，X. Chen等人提出了两阶段蚁群算法模型，该模型能够克服早熟收敛与最优路径之间的主要不一致性问题。

在文献[14-15]中，提出了一种基于蚁群优化的最优路径规划方法。将机器人视为一个点，使其在离散的工作环境表示中占有一个精确的单元。在模糊逻辑系统评价的代价函数中，考虑了路径的长度和导航的难度。该算法具有环境变化的自适应能力，可以实现具有动态障碍物的机器人全局路径规划。

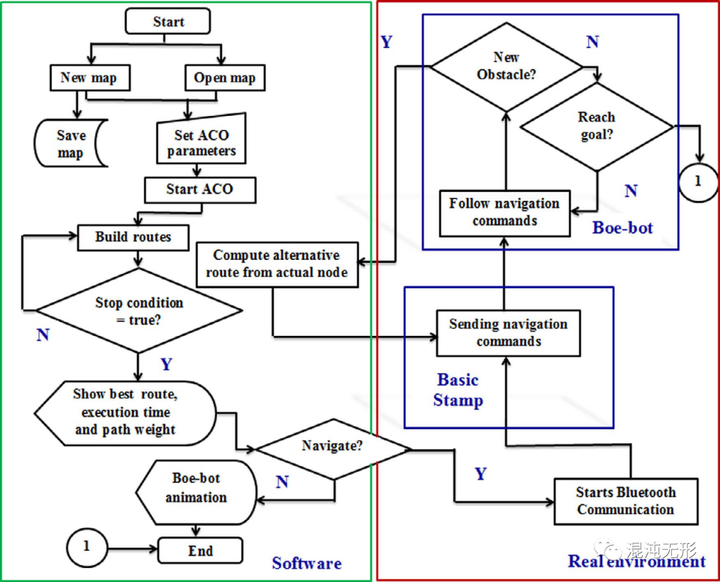
图 2.4 Fuzzy–ACO算法[15]

在文献[16]中提出了势场法(PFM)和ACO的结合规划方案。在混合算法中,采用PFM建立了确定性规划,然后使用ACO进行搜索最佳路由。结果表明,最优解的概率显著增加。

03智能仿生规划算法分析

上述三类智能仿生规划算法各有各的特点，接下来对比分析这三类规划算法的优缺点：

总体来看，仿生智能算法能够规划出最优或次优的路径，但它们的收敛速度是无法确定的，且其规划的时间一般较长，因此不适用于实时性要求高的应用场景，多数被应用于离线寻优计算，如物流配送规划、新药物结构探索等领域。

04结论与展望

本文将智能仿生规划算法拆解为三个子类算法：神经网络规划算法、模糊逻辑规划算法及基于仿生的规划算法，并沿时间先后顺序概述了相关类型算法的发展改进历程，接着从计算实时性、动态环境适应能力及学习能力等方面分析了上述三类算法的优缺点，并指出存在的相关问题。

运动规划算法种类繁多，应用场景各不相同，而本文仅概述分析了四类运动规划算法之一的智能仿生规划算法，后续会具体分析相关算法的应用案例。

（文章仅笔者个人分析，有误请指正，谢谢！）

参考资料

[1]REIF J, WANG H. The complexity of the two dimensional curvature-constrained shortest-path problem; proceedings of the Third International Workshop on Algorithmic Found

[2]E.A. Antonelo, B. Schrauwen, Supervised learning of internal models for autonomous goal-oriented robot navigation using reservoir computing, in:IEEE International Conference on Robotics and Automation, ICRA, Alaska, USA, 2010, pp. 2959–2964.

[3]D. Janglova, Neural networks in mobile robot motion, Int. J. Adv. Rob. Syst. 1 (2004) 15–22.

[4]M.A. Sagban, R. Dhaouadi, Neural-based navigation of a differential-drive mobile robot, in: Control Automation Robotics and Vision, ICARCV, 2012,pp. 353–358.

[5]I. Engedy, G. Horvath, Artificial neural network based mobile robot navigation, in: IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 2009, pp. 241–246

[6]H. Chang, T. Jin, Command fusion based fuzzy controller design for movingobstacle avoidance of mobile robot, in: Future Information Communication Technology and Applications, in: Lecture Notes in Electrical Engineering, 2013, pp. 905–913.

[7]A. Zhu, S.X. Yang, A fuzzy logic approach to reactive navigation of behaviorbased mobile robots, in: IEEE International Conference on Robotics and Automation, ICRA, New Orleans, LA, 2004, pp. 5045–5050.

[8]Y. Hu, S.X. Yang, A knowledge based genetic algorithm for path planning of a mobile robot, in: IEEE International Conference on Robotics and Automation, ICRA, New Orleans, LA, USA, 2004, pp. 4350–4355.

[9]S.C. Yun, S. Parasuraman, V. Ganapathy, Dynamic path planning algorithm in mobile robot navigation, in: IEEE Symposium on Industrial Electronics and Applications, Langkawi, Malaysia, 2011, pp. 364–369

[10]B.K. Oleiwi, R. Jarrah, H. Roth, B.I. Kazem, Multi objective optimization of trajectory planning of non-holonomic mobile robot in dynamic environment using enhanced GA by fuzzy motion control and A*, in: Neural Networks and Artificial Intelligence, in: Communications in Computer and Information Science, vol. 440, 2014, pp. 34–49

[11]Y. Zhang, D. Gong, J. Zhang, Robot path planning in uncertain environment using multi-objective particle swarm optimization, Neuron Comput. 103 (2013) 172–185.

[12]Y. Hao, W. Zu, Y. Zhao, Real-time obstacle avoidance method based on polar coordination particle swarm optimization in dynamic environment, in: 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 2007, pp. 1612–1617

[13]X. Chen, Y. Kong, X. Fang, Q. Wu, A fast two–stage ACO algorithm for robotic path planning, Neural Comput. Appl. 22 (2013) 313–319.

[14]M.A.P. Garcia, O. Montiel, O. Castillo, R. Sepulveda, Optimal path planning for autonomous mobile robot navigation using ant colony optimization and a fuzzy cost function evaluation, Adv. Soft Comput. 41 (2007) 790–798.

[15]M.A.P. Garcia, O. Montiel, O. Castillo, R. Sepulveda, P. Melin, Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation, Appl. Soft Comput. 9 (2009) 1102–1110.

[16]D. Zhao, J. Yi, Robot planning with artificial potential field guided ant colony optimization algorithm, Lecture Notes in Comput. Sci. 4222 (2006) 222–231.

[17]Mac T T , Copot C , Tran D T , et al. Heuristic approaches in robot path planning: A survey[J]. Robotics and Autonomous Systems, 2016, 86.

[18]A M N Z , B J C M . Methodology for Path Planning and Optimization of Mobile Robots: A Review - ScienceDirect[J]. Procedia Computer Science, 2018, 133:141-152.

福利放送

笔者为小伙伴们整理了期刊论文版式原文PDF，方便收藏和回味

链接：https://pan.baidu.com/s/1EvJ03sEOWpzEL6y2cndpKA

提取码：exmo

若链接失效，可在后台回复本文标题或发送邮件：Zippen-Huang@outlook.com

延伸阅读

-----------------------------------------------------------------------------

相关声明

1.如果转载本文，文末务必注明：“转自微信公众号：混沌无形”

2.若有侵权，请联系作者

全文完，感谢阅读！！如果觉得写的不错，那就点个赞或者“在看”吧。

上一篇介绍了遗传算法，本篇接着介绍应用于路径规划的另一种算法——粒子群算法（PSO），主要介绍算法的理论基础以及实现流程等。

粒子群算法是可应用于路径规划的一种常用算法，最早源于对鸟群捕食行为的研究。当一块区域内只有一块食物时，鸟群不知道食物的具体位置，但知道食物与他们自身的距离有多远。那么，鸟群找到食物的最优策略为：确定距离食物最近的鸟的距离，然后在其附近搜素。

粒子群算法的具体描述为：在空间中首先随机给出一群粒子，每个粒子都有自己的位置与速度属性，根据具体的优化目标，规定粒子的适应度计算函数，通过不断更新粒子的位置与速度属性进行迭代，将整个粒子群的最优适应度逐渐提高，最终得到近似的问题最优解。

（1）粒子群初始化

首先确定粒子群的粒子个数n，最大迭代次数max，设置粒子的位置和速度范围xlim，vlim，除此以外，需要确定学习因子c_1，c_2以及权重系数w的大小，用于第（3）步中粒子位置与速度属性的更新。

第一步的最后，还需要对种群中每个粒子的速度和位置进行初始化。初始化位置属性时，可采用在问题规定区域内随机生成的方式，初始化速度属性时，在速度限制范围内随机取值，即：

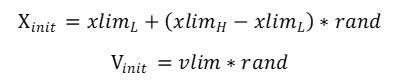
式中，xlim_H与xlim_L分别代表位置范围的上下限，rand为0到1之间的随机数。

（2）粒子群适应度计算

根据问题的优化目标，确定适应度函数。对路径规划问题，可将适应度函数设置为与路径长度负相关的函数，如：

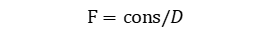
式中，cons为常数影响因子，可自行设置，D为路径长度。

确定适应度函数之后，对粒子群所有个体的适应度进行计算，根据结果对个体历史最优位置X_Pbest进行更新，同时确定当前种群的最佳适应度，并对整个粒子群的历史最优位置X_Gbest 进行更新。

（3）速度与位置属性更新

粒子群算法的速度与位置更新方式是确定的，具体过程如下：

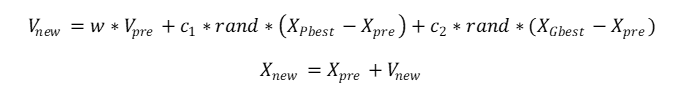
式中，下标为pre，new分别代表更新前，后的粒子属性，c_1，c_2，w，X_Pbest，X_Gbest以及rand同步骤（1），（2）中的定义。

更新后，需要考虑边界条件xlim与vlim，对X_new与V_new进行判断，若更新后的位置与速度属性超出边界，则将边界值作为新的位置/速度属性。

（4）记录最佳适应度值

将本代粒子群的最佳适应度值记录，并对历史最佳适应度值进行更新。

至此，一次迭代过程完成。

整个算法的实现流程如下图：

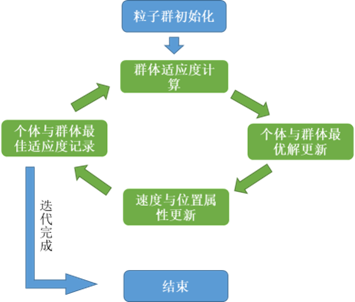
与上一篇中介绍遗传算法的示例相同，路径规划问题如图：

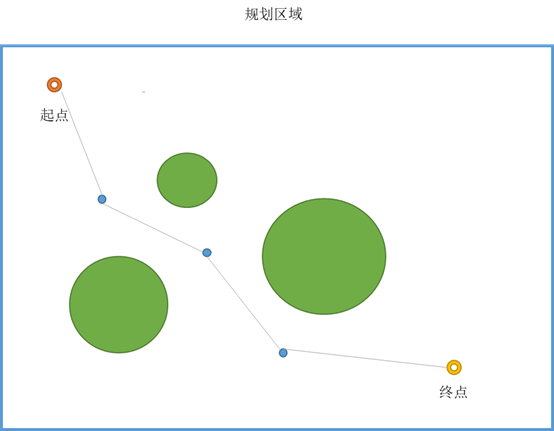
（1）粒子群初始化

对于此路径规划问题，可以用每个粒子的维度来表示路径中间点的个数，这里设置为dim，同时，规定每个维度由x,y两个坐标构成。

接着，在位置允许范围内，随机生成每个粒子dim个维度的横纵坐标，同时设置粒子的最大速度为V_max。

（2）适应度计算

与上一篇遗传算法中的流程相似，这里同样考虑到碰撞问题，规定相同的碰撞函数，故适应度函数设置为：

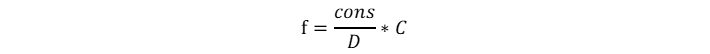
式中：C为碰撞因子，如果碰撞函数检测到路径与障碍物碰撞，则C为0，否则C为1。

（3）速度与位置属性更新

利用算法流程中步骤（3）中的更新式更新每一个粒子的速度与位置属性。

（4）最佳适应度更新

通过计算粒子群中每个个体的适应度值，对个体历史最佳适应度与群体历史最佳适应度进行更新。

（5）判断是否达到最大迭代次数，若不是则返回到步骤（2）继续迭代，若是则计算结束。

通过上一篇和本篇的介绍，可以发现，遗传算法与粒子群算法这两种算法在某些方面是相通的，这里对他们做一个比较：

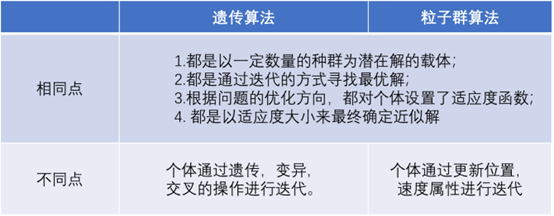
可以看出，两者的不同主要体现在个体的迭代方式上，粒子群算法相对遗传算法，迭代方式更简单，因此实现起来更方便。

本篇主要介绍了应用于路径规划中的另外一种算法——粒子群算法，介绍了算法的理论基础，实现流程，应用示例以及与遗传算法的比较。

到这里，算法补充板块就暂告一个段落了，希望对大家有所帮助。之后大家有什么想了解的，欢迎评论区留言呀~

最后，文章原创不易，期待大家的三连哦~

点赞——是你们对我最大的认可和鼓励~

收藏——方便大家之后需要的时候查找~

转发——分享给需要的小伙伴，大家一起进步~

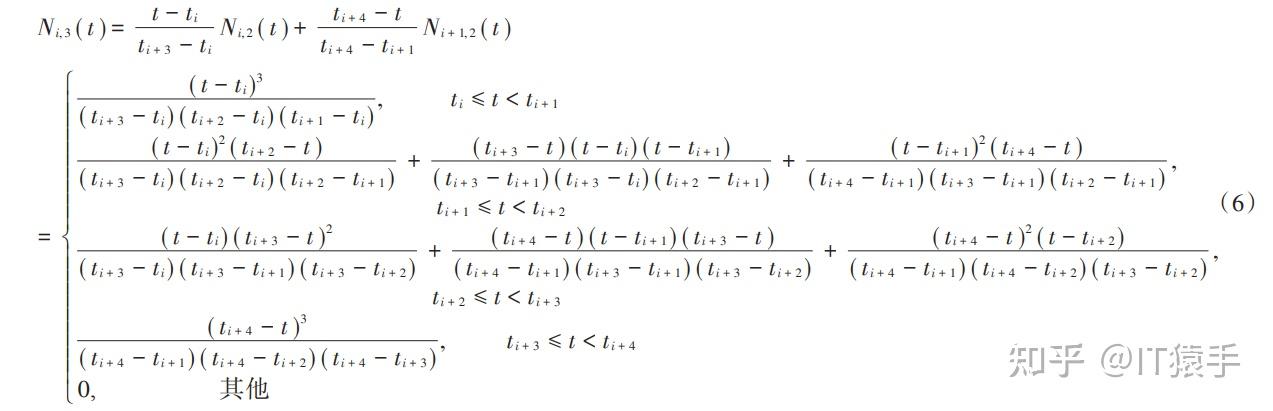
参考文献：

[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120

蜣螂优化算法（Dung beetle optimizer，DBO）由Jiankai Xue和Bo Shen于2022年提出，该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为的启发所得。

单目标优化：蜣螂优化算法（Dung beetle optimizer，DBO）_单目标优化算法_IT猿手的博客-CSDN博客

地形图可以随机生成，无人机起始点可以自己设定，算法的种群大小和迭代次数可以修改。

部分代码：

close all
clear  
clc
reference code link : https://mbd.pub/o/bread/ZJmck5tp
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
goalPos=[80, 90, 150]; %起点(可以修改)
startPos=[10, 10, 80]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F1'; %F1:随机产生地图 F2：导入固定地图
Max_iteration=50; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,curve]=DBO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
reference code link : https://mbd.pub/o/bread/ZJmck5tp
figure
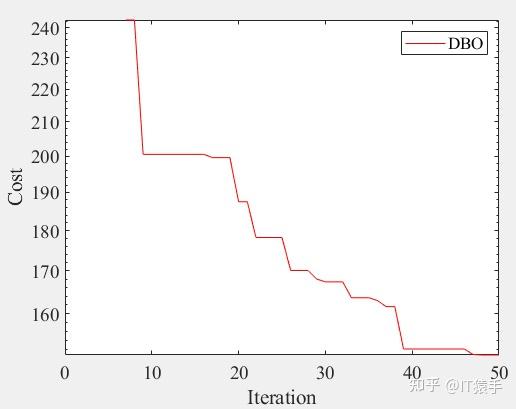
semilogy(curve,'Color','r')
xlabel('Iteration');
ylabel('Cost');
legend('DBO')
Position=[Best_pos(1:dim/3); Best_pos(1+dim/3:2*(dim/3)); Best_pos(1+(2*dim/3):end)]' %优化点的XYZ坐标（每一行是一个点）
display(['算法得到的最优适应度: ', num2str(Best_score)]);     
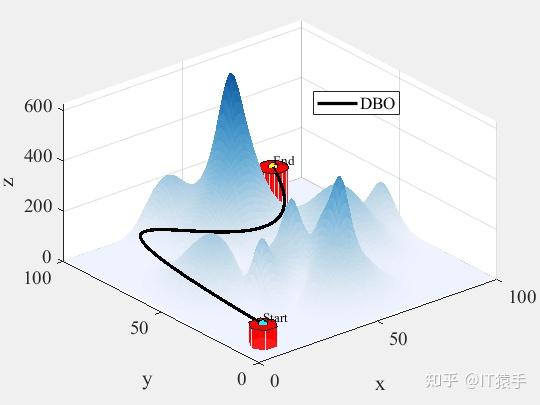
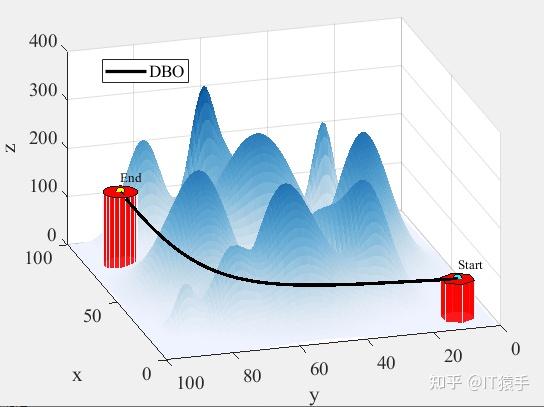
plotFigure(Best_pos)%画最优路径
reference code link : https://mbd.pub/o/bread/ZJmck5tp

部分结果：